Sequência de Fibonacci: o que é, como funciona e exemplos
A sequência de Fibonacci começa com 0 e 1 e segue com a soma dos dois números anteriores. A partir desta sequência é possível construir um retângulo, conhecido como Retângulo de Ouro, e também a Espiral de Fibonacci
Descrita pelo matemático italiano Leonardo Fibonacci no final do século XII, a sequência de Fibonacci é uma sucessão de números encontrada em alguns elementos da natureza. A sucessão começa com 0 e 1 e segue com a soma dos dois números anteriores, da seguinte forma: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34… A partir desta sequência é possível construir um retângulo, conhecido como Retângulo de Ouro, e também a Espiral de Fibonacci.
O italiano percebeu a sequência ao acompanhar a evolução, ao longo de um ano, de uma população de coelhos originada por um único casal. Caso nenhum coelho nesse processo, a sequência de infinita, começando com os números 0 e 1. Fibonacci observou que a quantidade de casais de coelhos cresceu segundo uma mesma ordem, mês a mês. A seguinte forma define a sequência percebida pelo matemático: Fn = Fn - 1 + Fn - 2.
Seja assinante O POVO+
Tenha acesso a todos os conteúdos exclusivos, colunistas, acessos ilimitados e descontos em lojas, farmácias e muito mais.
AssineA proporção áurea na sequência de Fibonacci
A partir do número 3 da sequência, é possível obter outra constante: a proporção (ou razão) áurea, utilizada na arte, na arquitetura e no design por sua agradabilidade aos olhos humanos. O valor da proporção áurea é de 1,618..., um número irracional e infinito representado pela letra grega phi. Quanto mais se avança na sequência de Fibonacci, mais a divisão entre um número e seu antecessor se aproxima desse valor.
A espiral de Fibonacci
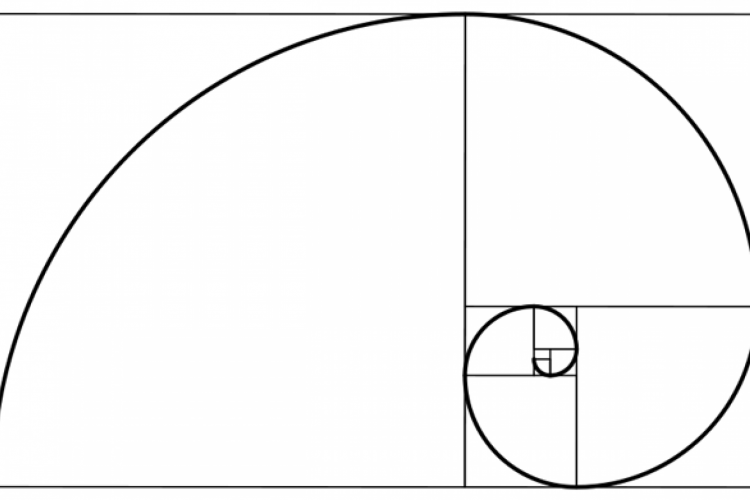
O desenho da espiral de Fibonacci funciona assim: se o maior quadrado da ilustração tiver 1,618 centímetros de lado, então o segundo maior, à direita, terá 1 cm. Dessa forma, a divisão do tamanho de um pelo outro resulta na razão áurea. Assim, qualquer par de quadrados escolhido na espiral seguirá a mesma proporção, fazendo do desenho uma repetição contínua de si mesmo em versões que vão diminuindo de tamanho gradativamente.
Sequência e espiral de Fibonacci na natureza e na arte
A sequência de Fibonacci pode ser encontrada em alguns elementos da natureza e da arte, representada ou não através da espiral. Confira:
- Um pedaço da concha de um caramujo tem o tamanho calculado pela soma dos dois antecessores;
- Quando contraído, o rabo de um camaleão é uma das representações mais precisas da espiral de Fibonacci;
- Se as presas de marfim de um elefante crescessem sem parar teriam como formato a espiral de Fibonacci;
- As sementes de um girassol, no miolo da flor, são organizadas em dois conjuntos de espirais: 21 no sentido horário e 34 no anti-horário;
- O mesmo acontece com as sementes de uma pinha: são oito no sentido horário e 13 no anti-horário;
- Se um ser humano de estatura mediana dividir sua altura pela distância entre o umbigo e a cabeça, o resultado será em torno de 1,618;
- A sequência de Fibonacci é percebida em “Mona Lisa”, de Leonardo da Vinci, na relação entre o tronco e a cabeça da personagem retratada, assim como nos elementos do rosto;
- A proporção áurea é o resultado da razão entre as estrofes maiores e menores da “Ilíada”, poema épico de Homero sobre a Guerra de Troia;
- A largura e a altura da fachada do tempo de Partenon, construído na Grécia no século V a.C., estão na proporção de 1 para 1,618;
- Cada bloco das Pirâmides do Egito é 1,618 vezes menor do que aquele logo abaixo.
Com informações de Superinteressante